ReadDigestOnPythonAlgorithm
Sep 26, 2016
Technology
目标
本节目标是:
* 理解算法分析的重要性
* 能使用"Big-O"描述算法的执行时间
* 理解常用的Python数组和字典的"Big-O"执行时间
* 理解Python数据的实现是如何影响到算法分析的
* 理解如何对简单的Python程序进行性能基准测试
算法分析
典型问题是: 当两个程序解决了同一个问题,然而看起来有差别的时候,如何得知一种方案确实优
于另一种?
理解:算法是用于解决针对某种输入的黑盒实现。某种算法可能针对多种不同程序,这取决于程序
的编写者及编程时使用的编程语言。
程序对比
两种累加器的实现:
清晰、明了的实现:
def sumOfN(n):
theSum = 0
for i in range(1,n+1):
theSum = theSum + i
return theSum
print(sumOfN(10))
糟糕的实现:
def foo(tom):
fred = 0
for bill in range(1,tom+1):
barney = bill
fred = fred + barney
return fred
print(foo(10))
为什么糟糕? 考虑到程序的可读性。
算法分析关注点
关注点在于基于对计算资源的量化,以评价算法的好坏。比较两种不同算法,评价出其优劣。譬如 ,如果一种算法在解决同一问题时使用了比另一种算法少得多的计算资源时,我们可以说该种算法 较为优秀。
量化指标: A. 基于该算法在解决问题时所需要用到的内存大小来量化。B. 基于该算法所需的执行 时间来量化。(算法的执行时间/运行时间).
用于量化函数sunOfN的算法优劣,我们可以使用benchmark。该benchmark使用python的time模块
。用于计算该程序的执行时间.
BenchMark
BenchMark求和程序:
import time
def sumOfN2(n):
start = time.time()
theSum = 0
for i in range(1,n+1):
theSum = theSum + i
end = time.time()
return theSum,end-start
for i in range(5):
print("Sum is %d required %10.7f seconds"%sumOfN2(10000))
运行结果:
$ python2 bench.py
Sum is 50005000 required 0.0014350 seconds
Sum is 50005000 required 0.0013280 seconds
Sum is 50005000 required 0.0012429 seconds
Sum is 50005000 required 0.0012109 seconds
Sum is 50005000 required 0.0012770 seconds
更改累加数的大小(10,10000,1000000?),可以看出程序执行时间的变化。
优化过后的算法,可以使用公式: sum = (n)*(n+1)/2来快速求累加值,代码如下:
import time
def sumOfN3(n):
start = time.time()
theSum = 0
theSum = (n*(n+1))/2
end = time.time()
return theSum,end-start
print("Sum is %d required %10.7f seconds"%sumOfN3(10))
print("Sum is %d required %10.7f seconds"%sumOfN3(10000))
print("Sum is %d required %10.7f seconds"%sumOfN3(100000))
print("Sum is %d required %10.7f seconds"%sumOfN3(1000000))
print("Sum is %d required %10.7f seconds"%sumOfN3(10000000))
print("Sum is %d required %10.7f seconds"%sumOfN3(100000000))
运行结果为:
$ python2 bench2.py
Sum is 55 required 0.0000019 seconds
Sum is 50005000 required 0.0000000 seconds
Sum is 5000050000 required 0.0000010 seconds
Sum is 500000500000 required 0.0000012 seconds
Sum is 50000005000000 required 0.0000010 seconds
Sum is 5000000050000000 required 0.0000000 seconds
BenchMark告诉我们的:直观的来看,使用迭代干的活更多,因而花费的时间更长。
随着N增大,迭代所需要花费的时间也随之增长。然而,这可能会导致问题,sumOfN3
在老旧架构的电脑上运行时,可能会花费更长的时间。
BenchMark提供给我们观察运行时间的方法,然而它取决于实际机器的运行情况、编程 语言、编译器等等诸多要素。而对于算法本身优劣而言,我们需要一种脱离于以上这些 制约要素的衡量方法。这种衡量方法应该仅仅针对于算法本身,在不同算法的实现之间 找寻出其优劣性。
Big-O表示法
如果需要独立于程序或者计算机等制约要素来衡量算法的效率,则需要量化出该种算法 所需要执行的步骤或操作。如果这些步骤被视为计算的基本单元,那么一种算法的执行时间 则可以被表述为解决此问题所需的步骤个数。决定出一种恰当的计算基本单元是衡量算法时 的难点之一,且取决于该算法是如何被实现的。
sumOfN的实现为:
theSum = 0
theSum = theSum + i
可被描述为T(n) = 1+n, 可被解读为"T(n)是用来解决问题的时间,大小为n,1+n步”
按照上述描述,不难理解累加到100,000的执行时间要大于累加到1,000的时间。
计算机科学家对分析方法会更进一步,当问题变大时,T(n)的某些部分会主导其他部分。 这种占主导部分的行为将用于算法优劣的比较。量级函数描述了T(n)中随着n增加而 增长最快的部分。量级函数通常被称之为Big-O表示法。O(f(n)).
T(n)=1+n中,当n增大时,1可以被忽略,因而执行时间就是O(n). 1也是很重要的,然而随着 n的增大,没有1计算结果也会近似于n.
再比如T(n) = 5n^2 + 27n + 1005, 在n大小为1或2时,1005常量主导,然而随着n的增大 很显然n^2会占主导地位,以至于系数5都可以被忽略,所以T(n)的Big-O表示为O(n^2).
算法执行时,会有最坏情况和平均情况。算法的表现和特定的数据集有关系。一般情况下 会处于两种极端之间,即处于平均情况。
截图,常用的Big-O函数列表

各种函数列表的图示:
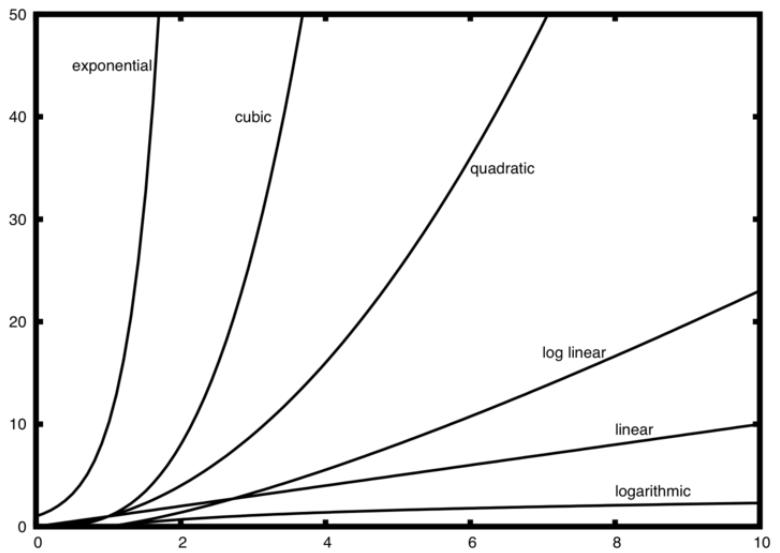
n不大时,各种算法优劣相差不大,然而n增大时,很容易看到各自之间的差别。
实际分析, T(n)=3+3n^2+2n+1=3n^2+2n+4.
查看指数,我们容易得到n^2处于主导地位,因而算法的复杂度应该用O(n^2)来表示。注意其他部分 包括系数都可以随着n的增大而被忽略。
图示:
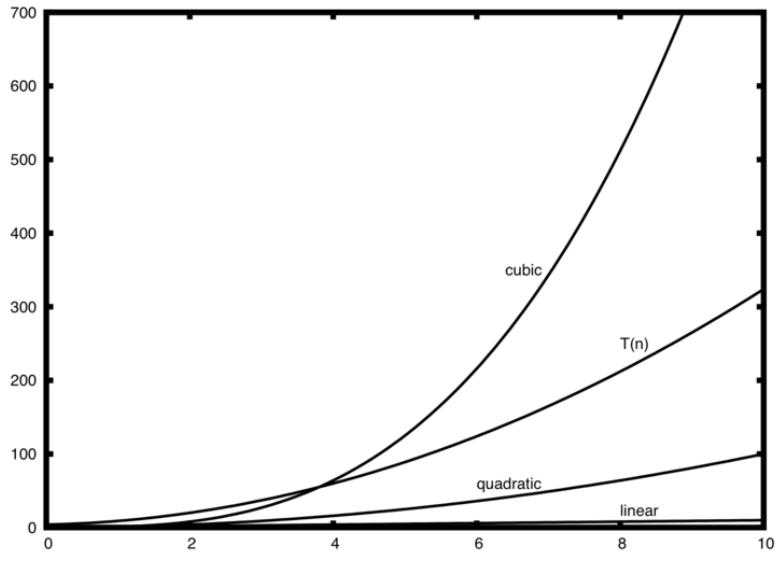
字谜检测例子
看两个字符串中蕴含的单个字符是否相同,例如heart和earth是相同的。具体的代码实现如下:
def anagramSolution1(s1,s2):
alist = list(s2)
pos1 = 0
stillOK = True
while pos1 < len(s1) and stillOK:
pos2 = 0
found = False
while pos2 < len(alist) and not found:
if s1[pos1] == alist[pos2]:
found = True
else:
pos2 = pos2 + 1
if found:
alist[pos2] = None
else:
stillOK = False
pos1 = pos1 + 1
return stillOK
print(anagramSolution1('abced','dcbae'))
在s1中的n个字符,将触发对s2中的n个字符的迭代。也就是说,s2中的n个字符将被访问一次, 以匹配s1中的任一字符。O(n^2)为其复杂度。
改进后的方案,先排序,后比较。
def anagramSolution2(s1,s2):
alist1 = list(s1)
alist2 = list(s2)
alist1.sort()
alist2.sort()
pos = 0
matches = True
while pos < len(s1) and matches:
if alist1[pos]==alist2[pos]:
pos = pos + 1
else:
matches = False
return matches
print(anagramSolution2('abcde','edcba'))
看上去n次比较就够了,似乎应该是O(n),然而排序需要算法复杂度。排序通常有O(n^2)或是 O(nlogn)。因而这个例子由排序的复杂度来决定。
第三种方法是穷举,Brute Force(蛮力)。我们用s1的字符,生成所有可能的字符串,然后看 s2是否在这些字符串中。则第一个位置有n种可能,紧接着n-1,n-2等等,结果是n的阶乘。
n!远大于2^n,譬如如果s1有20个字符,那么有20!种可能结果,用普通家用计算机,不太现实。 因而穷举在这里不符合。
第四种方法,对字符计数,而后对计数后的结果比较。因为仅仅有26个字符,因而用一个26长度 的数组来计算就好了。
代码:
def anagramSolution4(s1,s2):
c1 = [0]*26
c2 = [0]*26
for i in range(len(s1)):
pos = ord(s1[i])-ord('a')
c1[pos] = c1[pos] + 1
for i in range(len(s2)):
pos = ord(s2[i])-ord('a')
c2[pos] = c2[pos] + 1
j = 0
stillOK = True
while j<26 and stillOK:
if c1[j]==c2[j]:
j = j + 1
else:
stillOK = False
return stillOK
print(anagramSolution4('apple','pleap'))
没有嵌套的循环,首先用两个迭代数出字符数。第3个循环则是比较两个数字的列表,看是否 相等。因而最终的次数是2n+26次,则可以判断出是否是字谜。算法的复杂度是O(n)
对空间的要求,最后的解决方案是线性时间的,但是需要使用到额外的空间来存储两个列表。 牺牲了空间,换来了时间。
很多时候需要考虑空间和时间,例如,如果比较UTF字符,则需要考虑到是否可以用这种方法。
列表
python中列表的算法复杂度:
import timeit
from timeit import Timer
def test1():
l = []
for i in range(1000):
l = l + [i]
def test2():
l = []
for i in range(1000):
l.append(i)
def test3():
l = [i for i in range(1000)]
def test4():
l = list(range(1000))
t1 = Timer("test1()", "from __main__ import test1")
print("concat ",t1.timeit(number=1000), "milliseconds")
t2 = Timer("test2()", "from __main__ import test2")
print("append ",t2.timeit(number=1000), "milliseconds")
t3 = Timer("test3()", "from __main__ import test3")
print("comprehension ",t3.timeit(number=1000), "milliseconds")
t4 = Timer("test4()", "from __main__ import test4")
print("list range ",t4.timeit(number=1000), "milliseconds")
运行结果:
('concat ', 1.8388030529022217, 'milliseconds')
('append ', 0.09388995170593262, 'milliseconds')
('comprehension ', 0.042823076248168945, 'milliseconds')
('list range ', 0.01230001449584961, 'milliseconds')
concate的结果为O(k),k为数组的大小。
算法复杂度:
Operation Big-O Efficiency
index [] O(1)
index assignment O(1)
append O(1)
pop() O(1)
pop(i) O(n)
insert(i,item) O(n)
del operator O(n)
iteration O(n)
contains (in) O(n)
get slice [x:y] O(k)
del slice O(n)
set slice O(n+k)
reverse O(n)
concatenate O(k)
sort O(n log n)
multiply O(nk)
pop()与pop(n)的例子:
from timeit import Timer
import timeit
popzero = Timer("x.pop(0)",
"from __main__ import x")
popend = Timer("x.pop()",
"from __main__ import x")
print("pop(0) pop()")
for i in range(1000000,100000001,1000000):
x = list(range(i))
pt = popend.timeit(number=1000)
x = list(range(i))
pz = popzero.timeit(number=1000)
print("%15.5f, %15.5f" %(pz,pt))
运行结果:
$ python2 timer.py
pop(0) pop()
1.39908, 0.00019
2.87106, 0.00018
4.65139, 0.00018
6.42484, 0.00018
7.80698, 0.00018
9.34029, 0.00016
10.97498, 0.00017
12.16070, 0.00018
字典
算法复杂度如下:
operation Big-O Efficiency
copy O(n)
get item O(1)
set item O(1)
delete item O(1)
contains (in) O(1)
iteration O(n)
测试代码:
import timeit
import random
for i in range(10000,1000001,20000):
t = timeit.Timer("random.randrange(%d) in x"%i,
"from __main__ import random,x")
x = list(range(i))
lst_time = t.timeit(number=1000)
x = {j:None for j in range(i)}
d_time = t.timeit(number=1000)
print("%d,%10.3f,%10.3f" % (i, lst_time, d_time))
运行结果为:
$ python2 dic.py
10000, 0.160, 0.001
30000, 0.339, 0.001
50000, 0.570, 0.001
70000, 0.801, 0.001
90000, 1.037, 0.001
110000, 1.273, 0.001
130000, 1.470, 0.001
150000, 1.685, 0.001
170000, 1.961, 0.001
190000, 2.214, 0.001
210000, 2.574, 0.001
230000, 2.781, 0.001
250000, 3.094, 0.001
更多算法复杂度,可以参考python官方文章:
